Основна терминология. Стандартизация

Bulgarian
Medical Statistics
Medicine | 2nd year
Dental medicine | 2nd year
Материалът представя основната терминология за екстензивни и интензивни показатели както и метода на директна стандартизация.
Автор

Костадин Костадинов

Публикувано

November 3, 2024

Защо учим статистика?

  • Статистиката е метод чрез който данните се превръщат в информация.
  • Статистиката помага в ежедневната медицинска практика, чрез създаване на клинични наръчници или политики в здравеопазването.
  • Статистиката е езикът на науката, тя помага както на пациентите, така и за поддържане на здравето в обществото.

С какво ще ни помогне статистиката?

  • Да взимаме информирани решения в ежедневната ни практика.
  • Да разберем как работи науката.
  • За да четем критично нова научна информация.

Какво няма да научите?

Понастоящем статистиката е основата на “науката за данните” и изкуствения интелект (data science). В съчетание със сложна математика, програмиране и доза креативност, тази нова дисциплина навлиза във всекидневния ни живот докато пазаруваме, учим и работим. Всички технологии базирани на “изкуствен интелект” същност използват статистика 1 . В този курс, обаче целта е да придобиете най-основните знания за това как работи статистиката, каква е логиката в нея и какъв език използва.

Терминология

За да “не сме изгубени в превода”, въвеждаме някои основни термини, обяснени с примери.

Абсолютни величини

Определение

Това са числа, които количествено характеризират обемите на статистическите съвкупности или на части от тях. Те представляват стойност на конкретни статистически признаци.

  • Абсолютните величини са винаги наименовани с конкретни мерни единици.

  • Статистическите изследвания, обикновено започват с анализ на абсолютните величини, но те не са достатъчни за директни сравнения в пространствено-времеви аспект.

Примери за абсолютни величини

Систолното артериално налягане измерено в mmHg е абсолютна величина - има числова стойност, мерна единица и количествено характеризира определен признак. Кръвната захар измерена в mmol/l също е абсолютна величина - отново е число с мерна единица и измерващо конкретен показател.

Относителни величини

Определение

Те се изчисляват при разделяне на две абсолютни величини. Представят се като коефициенти, а при умножение по 100 или 1000 в проценти или промили.

Примери за относителни величини

В медицината, често използваме относителни величини. Например, когато измерваме помпената функция на сърцето можем да измерим количеството кръв, което постъпва в аортата, след едно сърдечно съкращение. Това е абсолютната величина ударен обем. Хората с по-висок ръст и по-високо тегло (по-едро телосложение) имат по-високи стойности на усърдния обем, спрямо тези с по-нисък ръст и по-малко тегло. Така например сърцето на състезател по сумо изтласква по-голямо количество кръв (в милилитри), спрямо сърцето на първокласник. Означава ли това, че сърцето на сумиста работи по-добре от това на първокласника? Отговорът е, че не можем да преценим - двете абсолютни величини не бива да се сравняват директно. Затова по-важното, в случая е съотношението на ударният обем, спрямо количеството кръв налично в сърцето, точно преди неговото съкращение. Това е т.н “фракция на изтласкване” и представлява относителна величина.

Екстензивни показатели

Определение

Това са структурни показатели, които показват как едно статистическо явление се разпределя на съставните си части в определено време и място.

Примери за екстензивни показатели

Ако приемем “възрастта” в гр. Пловдив за статистическо “явление” можем да представим всички жители на града в категории по възрастова група - новородени до 1 г., деца между 1 и 5 год., от 5 до 10 г. и т.н. Ако разделим броя на хората в съответната възрастовата група, спрямо всички жители на града ще получим екстензивен показател - измерен в процент. На Фигура 1 e представено разпределението на възрастта в гр. Пловдив. 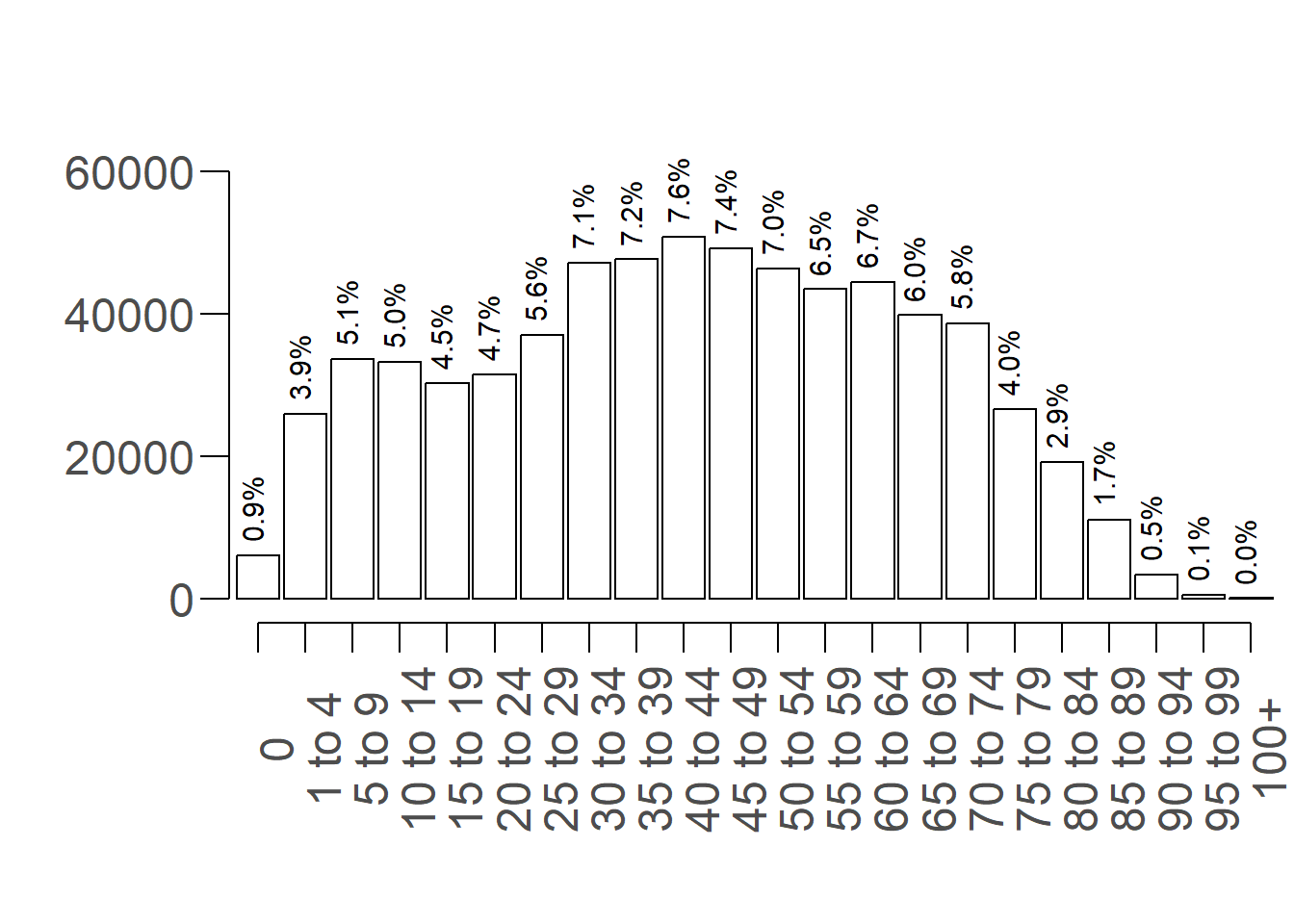Важно за екстензивните показатели е, че сумата от всички тях е равна на 1 (или 100%).

Фигура 1: Пример за екстензивен показател.Възраст на населението в гр. Пловдив, 2022 г.

Интензивни показатели

Определение

Това са честотни показатели, които показват колко често се среща дадено явление в свойствената си среда. Всеки интензивен показател е съотношение между обемите на две различни статистически съвкупности, намиращи се във връзка една с друга. В числителя е явлението от което се интересуваме, а в знаменателя е абсолютният обем на средата, в която възниква то.

Примери за интензивни показатели

  1. Леталитетът представлява броя смъртни случаи от конкретно заболяване, спрямо общия брой болни от това заболяване. Ако леталитетът от морбили (дребна шарка) при деца (до 18 г.) е 5%, това означава, че от 100 деца със заболяването, 5 са починали. С други думи, показателят представя честотата на една статистическа съвкупност (смъртните случаи) върху друга съвкупност (болните деца).

  2. Смъртността представлява съотношение на броя на починалите, спрямо средния брой население. Смъртността по причини представлява броя на починалите от дадено заболяването, разделен на броя на всички починали. Двата показателя не бива да се бъркат с леталитета.

  3. Заболеваемостта, представлява съотношението на броя новозаболели от дадено заболяване (например от рак на гърдата), спрямо популацията в риск (всички, които биха могли да се разболеят от това заболяване).

  4. В ежедневната практика като лекари, също ще ползвате интензивни показатели. Например, при пациенти с белодробна астма, видът на използваното лечение, зависи от честотата на екзацербации (обостряния) т.н интензивния показател “exacerbation rate”.

Пряк метод на стандартизация

Преди определението за стандартизация, нека представя следния пример пример. Представете си, че от днес сте министър на здравеопазването. Изправени сте пред сериозен проблем - в държавата върлува опасен вирус. Имате ваксина, но липсва доверие на гражданите в нея. Много хора смятат, че ваксините дори убиват. Днес след среща с граждани, противопоставящи се на ваксините, получавате научна статия, в която се твърди, че ваксините повишават вероятността от смърт. В Таблица 1 можете да видите данните от нея.

Таблица 1: Таблица на антиваксарите
Общо Починали
Ваксинирани 4000 2850
Неваксинирани 8000 5500

Авторът посочва, че след 1 година от 4000 ваксинирани са починали 2850 души, докато при 8000 неваксинирани, починали са 5500. Тези числа представляват абсолютни величини. За да се сравнят, трябва да използваме относителни. С други думи, каква пропорция от ваксинираните са починали, спрямо тази при неваксинираните. “Сметката” тук е лесна: трябва да разделим броя на починалите сред ваксинираните, върху общият брой на ваксинираните. Същата пропорция трябва да изчислим и за неваксинираните. Резултатите са относителни величини - интензивни показатели.

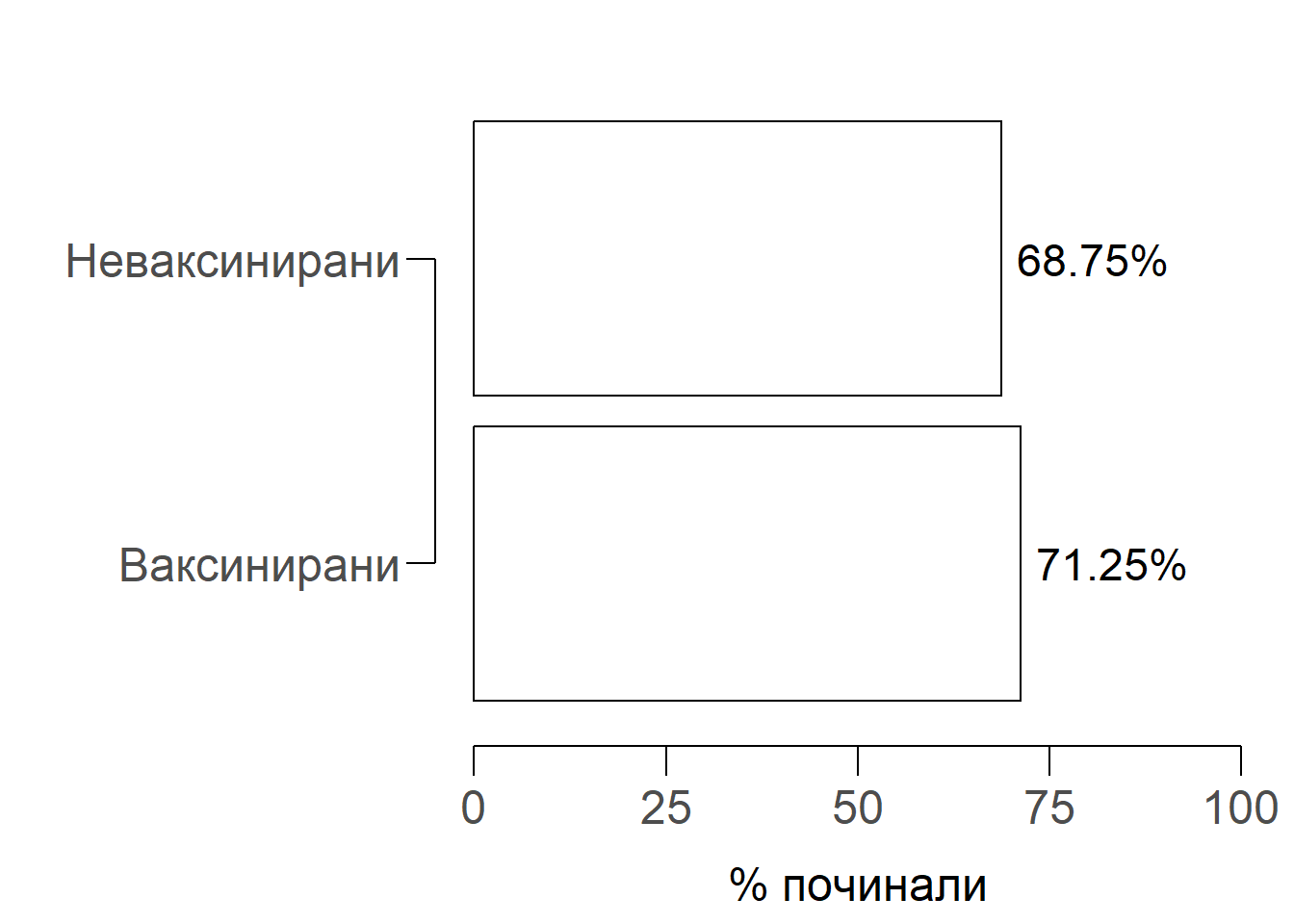
Разлика между смъртността при ваксинирани и неваксинирани.

Оказва се, че в групата на ваксинираните починалите са 71.2%, докато при неваксинираните - 68.8%. Това е разлика от 2,4 процентни пункта2. Може би, наистина “антиваксърите” имат право.

Как бихме могли да си обясним този резултат? Нима наистина ваксините са причина за по-големия брой смъртни случай? Трябва ли да продължим да използваме тази ваксина? Бихте ли посъветвали пациентите си да се ваксинират?

Преди да дадем категоричното си решение, трябва да помислим върху данните. Те все още не са информация, на която да базираме решенията си. В случая, можем да разглеждаме цифрите в таблицата, като сурови данни измерващи една връзка. Това е връзката между ваксинация и смъртен изход. Не изглежда логично, смъртта да се причинява единствено от ваксината или липсата на такава. Има редица други фактори, които могат да повлияят - например възрастта. Нормално е, ако ваксинираните са по-възрастни спрямо неваксинираните, при тях да наблюдаваме повече починали, дори и ако ваксината наистина работи и ефективна.

При сравняването на интензивни величини се наблюдава фактът, че стойността на тези показатели е в зависимост от структурата на средата, в която са изучавани явленията. За да проверим дали тази среда “замъглява” връзката между фактора и резултата, можем да използваме статистическия метод на стандартизацията.

Определение

Под стандартизация се разбира преобразуването на общите коефициенти, с което се отстранява (елиминира) влиянието на възрастови или други различия в състава на сравняваните групи.

Стъпки

За да извършим стандартизация (в курса по статистика се спираме единствено на прекия метод за стандартизация) следва да разполага с повече данни. Таблицата, която разгледахме, не съдържа информация за възрастта на участниците. Затова, след запитване към автора, получаваме по-подробни данни - представени в Таблица 2.

Възраст Общо Починали
Ваксинирани под 24 г. 500 250
25-34г. 500 300
35-44г. 1000 700
над 45г. 2000 1600
Неваксинирани под 24 г. 4000 2400
25-34г. 2000 1400
35-44г. 1000 800
над 45г. 1000 900
Таблица 2: Таблица с разпределние по възраст

Може би, ви прави впечатление от Фигура 2, че ваксинираните, са предимно по-възрастни хора, докато при неваксинираните преобладават по-младите.

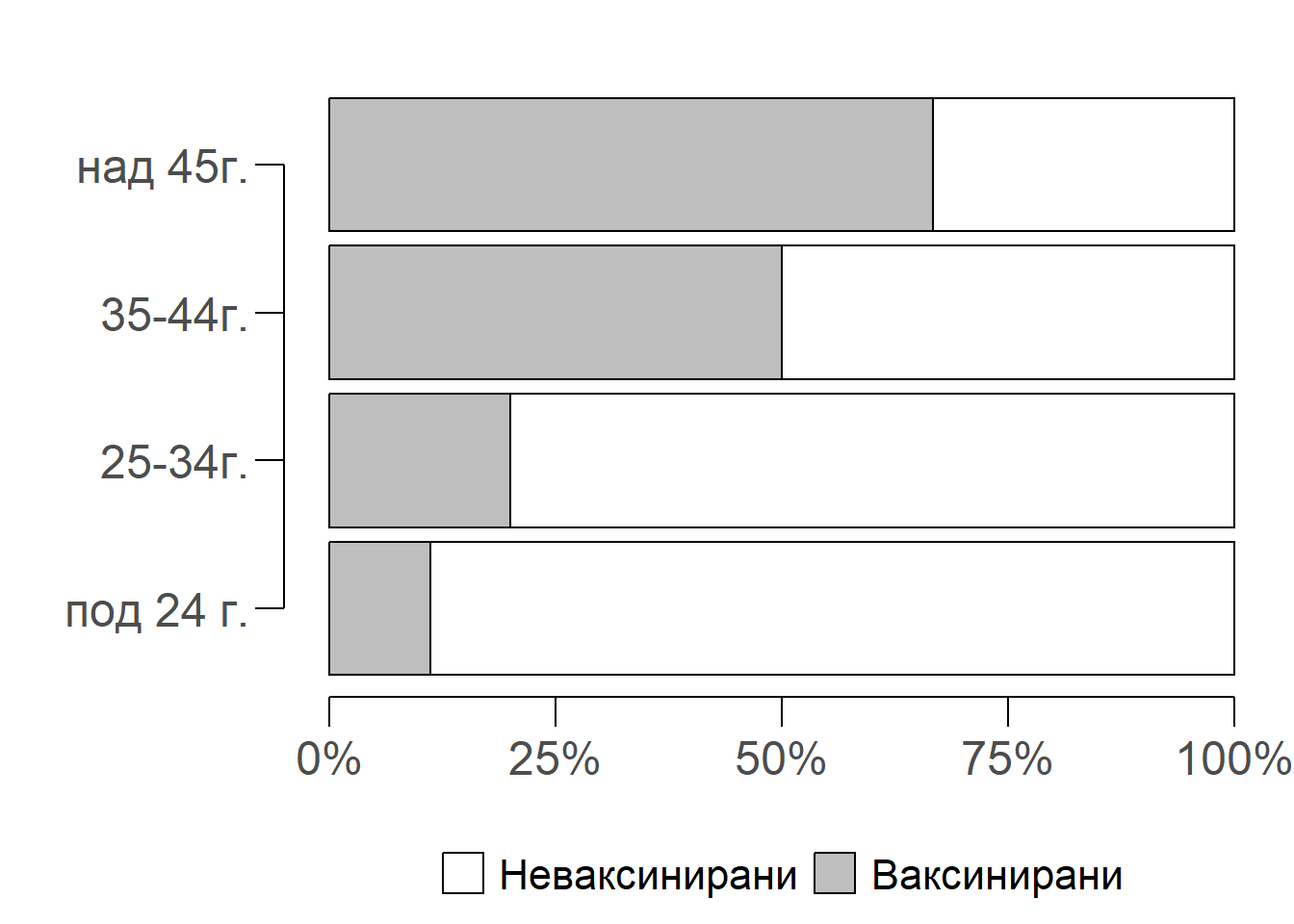
Фигура 2: Разлика на възрастовата структура между ваксинирани и неваксинирани - възрастовите групи са представени от млади към стари.в групата до 24 г. преобладат неваксинирани, докато при над 45-годинишните ваксинираните

Стъпка 1 Изчисляване на нестандартизираните интензивни показатели

Както по-рано, така и сега, можем да изчислим, какъв процент от участниците в двете групи са починали. В случая ще направим това за всяка една възрастова група. Резултатите са представени в колона леталитет в Таблица 3 .

Възраст Общо Починали Леталитет1
Ваксинирани под 24 г. 500 250 0.5
25-34г. 500 300 0.6
35-44г. 1000 700 0.7
над 45г. 2000 1600 0.8
Неваксинирани под 24 г. 4000 2400 0.6
25-34г. 2000 1400 0.7
35-44г. 1000 800 0.8
над 45г. 1000 900 0.9
1 Нестандартизиран
Таблица 3: Нестандартизиран леталитет. Тук е важно да запомним, че общият нестандартизиран показател не е сума от резултатите по групи. Не можем да сумираме нестандартизираните показатели.

Стъпка 2 Изчисляване на “стандарт”

За да направим стандартизацията е необходимо да изберем за стандарт, една от двете възрастови структури - тази на ваксинираните или тези на неваксинираните.

Тук, често възниква въпросът коя структура трябва да изберем? Защо да предпочетем едната спрямо другата? Какво е правилото?

Всъщност, няма особено значение точно коя структура се избира. Разбира се, числата след стандартизация зависят от избора и те биха се различавали. От значение, обаче е разликата, а не конкретните стойности на стандартизиран леталитет в двете групи 3

Какво обаче е стандартът?

Ако изберем за стандарт групата на неваксинираните, за да изчислим стандарта - ще използваме броя на участниците във всяка възрастова група за числител, а общия брой неваксинирани за знаменател. Полученият коефициент е “стандарт” за конкретната възрастова група.

В Таблица 4 са представени получените стандарти.

Неваксинираните участниците под 24 год. са 4000, а общият брой неваксинирани 8000. Стандартът за тази група е 0.5 (ако умножим по 100 ще получим 50%). Това е стандартът за тази група, които обаче ще използваме и за ваксинираните.

Може да ви направи впечатление, че сборът на всички стандарти е равен на 1-ца (тоест 100%). Това е така, защото стандартът винаги е екстензивен показател.

Възраст Общо Починали Стандарт1
под 24 г. 4000 2400 0.500
25-34г. 2000 1400 0.250
35-44г. 1000 800 0.125
над 45г. 1000 900 0.125
1 За изчисляване на колоната стандарт е изпозлвана възрастовата структура на неваксинираните
Таблица 4: Определяне на стандарт за всяка възрастова група

Стъпка 3: Изчисляване на стандартизираните показатели

За да изчислим стандартизираният леталитет, за всяка възрастова група умножаваме нестандартизирания показател по посоченият по-горе стандарт.

Таблица 5: Например, за възрасттовата група до 24 г. при ваксинираните, нестандартизираният леталитет е 0,5, а стандартът 0,500 . За да стандартизираме умножаваме 0,5 по 0.500. При неваксинираните, отново за същата възрастова група, умножаваме нестандартизирания показател 0,6 по стандарта 0,500
Възраст Общо Починали НС Леталитет1 Стандарт2 С Леталитет3
Ваксинирани под 24 г. 500 250 0.5 0.500 0.2500
25-34г. 500 300 0.6 0.250 0.1500
35-44г. 1000 700 0.7 0.125 0.0875
над 45г. 2000 1600 0.8 0.125 0.1000
Неваксинирани под 24 г. 4000 2400 0.6 0.500 0.3000
25-34г. 2000 1400 0.7 0.250 0.1750
35-44г. 1000 800 0.8 0.125 0.1000
над 45г. 1000 900 0.9 0.125 0.1125
1 Нестандартизиран леталитет
2 Изчислен спрямо неваксинираните
3 Стандартизиран леталитет

На този етап стандартизацията е почти изпълнена - Вече знаем, че нестандартизираните показатели не се събират. За сметка на това стандартизираните се събират. Когато ги съберем получаваме общия стандартизиран леталитет, който е “изчистен” от замъгляващия ефект на различната възраст в двете групи. С други думи, показателите след стандартизация, представят какъв би бил леталитетът, ако двете групи имаха еднаква възрастова структура.

Стъпка 4: Заключение

Нека извършим тази последна калкулация.

За групата на ваксинираните общият стандартизиран леталитет е:

  • 25 % (стандартизираният леталитет за всички до 24 г.) + 15 % (стандартизираният леталитет за възрастовата група от 25-34 г.) + 8,7 % (стандартизираният леталитет за възрастовата група от 35-44 г.) + 10 % (стандартизираният леталитет за възрастовата група над 45 г.). Общо за всички ваксинирани, стандартизираният леталитет е 58.7%

За групата на неваксинираните общият стандартизиран леталитет е:

  • 30 % (стандартизираният леталитет за всички до 24 г.) + 17,5 % (стандартизираният леталитет за възрастовата група от 25-34 г.) + 10 % (стандартизираният леталитет за възрастовата група от 35-44 г.) + 11,25 % (стандартизираният леталитет за възрастовата група над 45 г.). Общо за всички ваксинирани, стандартизираният леталитет е 65.75%
Заключение

Стандартизираните показатели за леталитет в двете групи са съответно 58.75 % и 68.75 %. Леталитетът сред неваксинираните, е с 10 % по-висок.

Стандартизираните показатели позволяват да се анализира и оцени нивото на изучаваното явление при създадени условия на еднородност, тоест методът ни показва какви биха били коефициентите, в сравняваните групи, ако те имаха еднакъв състав.

Стъпки - при алтернативен избор за стандарт

За да докажем, че изводът не зависи от избора на стандарт, ще решим отново примера, като този път използваме за стандарт възрастовата структура на ваксинираните.

Стъпка 2 Изчисляваме стандарта (този път спрямо ваксинираните)

Сега ще използваме данните само за ваксинираните. При тях, частниците под 24 г. са 500 от общо 4000. Това означава, че стандартът за тази група е 0.125 (или 12.5%). Получените стандарти са представени в Таблица 6 .

Възраст Общо Починали Стандарт1
под 24 г. 500 250 0.125
25-34г. 500 300 0.125
35-44г. 1000 700 0.250
над 45г. 2000 1600 0.500
1 За изчисляване на колоната стандарт е изпозлвана възрастовата структура на ваксинираните
Таблица 6: Определяне на стандарт за всяка възрастова група

Стъпка 3: Изчисляване на стандартизираните показатели за леталитет

След като имаме “стандарт”, този път в основа на групата на ваксинираните, можем да пристъпим отново към стъпка 3 - стандартизация тя е представена в Таблица 7

Таблица 7: Отново, за възрасттовата група до 24 г.при ваксинираните, нестандартизирания леталитет е 0,5, а новият стандарт 0,125. Стандартизираният леталитет е 0,5x0,125 = 0,0625. При неваксинираните, до 24 г. нестандартизирания леталитет е 0,6, за да получим стандартизирания умножаваме по стандарта 0,125, получаваме 0,075)
Възраст Общо Починали НС Леталитет1 Стандарт2 С Леталитет3
Ваксинирани под 24 г. 500 250 0.5 0.125 0.0625
25-34г. 500 300 0.6 0.125 0.0750
35-44г. 1000 700 0.7 0.250 0.1750
над 45г. 2000 1600 0.8 0.500 0.4000
Неваксинирани под 24 г. 4000 2400 0.6 0.125 0.0750
25-34г. 2000 1400 0.7 0.125 0.0875
35-44г. 1000 800 0.8 0.250 0.2000
над 45г. 1000 900 0.9 0.500 0.4500
1 Нестандартизиран леталитет
2 Изчислен спрямо неваксинираните
3 Стандартизиран леталитет

Логично, след като сме използвали друг стандарт, числовите стойности са различни, но заключението едно и също.

Заключение

Стандартизираните показатели за леталитет в двете групи са съответно 71.25 % и 81.25 %. Леталитетът сред неваксинираните, е с 10 % по-висок.

Задачи за самоподготовка

  1. Да се определи възрастовата структура на преминалите болни през Болница Х, като разполагате със следните данни:
Възраст 0-1 г. 1-4 г. 5-9 г. 10-19 г. Общо
Болни с Хепатит А 70 41 102 87 300
Възрастова структура (%)
  1. Да се изчислят стандартизираните показатели за плодовитостта в районите А и Б. За стандарт да се приеме възрастовият състав на жените от район Б. Да се анализират получените резултати.
Район А Район Б
Възраст Жени Живородени Жени Живородени
15-19 1 000 18 1 200 22
21-30 9 000 225 7 000 175
31-49 8 000 128 10 000 160
Всичко 18 000 371 18200 357
  1. Да се изчислят стандартизираните показатели за леталитета в две градски болници - Болница А и Болница Б. За стандарт да се приеме съставът на болните в болница Б. Да се анализират получените резултати.
Болест

Преминали

(А)

Починали

(А)

Преминали

(Б)

Починали

(А)
Хипертонична болест 180 4 200 4
Рак на стомаха 100 30 90 27
Инфаркт на миокарда 120 8 160 10
Всичко 400 42 450 41
  1. Нестандартизираните показатели за леталитет в две болници А и Б са съответно 10‰ и 12‰. След стандартизация, спрямо болница А, леталитетът в болница А е 10‰, а този в болница Б 8‰. Изчислете стандартизираните леталитети, ако за стандарт се ползва болница Б.

Бележки

  1. В момента дори има разработени скенери които “сами разчитат” дали пациента има заболяване и показват какво е то. Разработени са и електрокардиографии, записващи сърдечната дейност на пациента и “автоматично” разпознаване дали е налице определено заболяване.↩︎

  2. Важно: простите аритметични операции между проценти се изразяват в процентни пунктове.↩︎

  3. В това упражнение ще докажем това, като извършим стандартизацията, като вземем за стандарт, първо възрастовата структура на неваксинираните, а после тази на ваксинираните.↩︎