Увод
Често при представяне на статистически данни сме податливи на бързи заключения за връзката между две или повече явления. Наличието на статистическа връзка е особено важно за медицината, тъй като тя е основна при определянето на конкретен фактор за “рисков” за развитието на определено заболяване. Въпреки това способността ни да изграждаме “причинно-следствени” вериги понякога ни “заблуждава”. Човешкият мозък е склонен да мисли за две явления като свързани, дори и в действителност такава връзка да липсва. Не бива да се смята, че статистическа и причинно следствена свръзка са едно и също понятие. Дори напротив, резултатите от статистическия анализ сами по себе си не могат да се разглеждат като изчерпателно доказателство в подкрепа на тезата за причинната обусловеност 1.
Вероятността дадена връзка да бъде причинно-следствена е по-голяма:
- Когато тя е по-силна и характеризира се с високи стойности за статистическите коефициенти;
- Когато тя е правдоподобна от биомедицинска гледна точка. Научните (теоретични, експериментални) данни и доказателства за механизма на взаимодействията са основни аргументи в полза на причинността. Изясняването на правдоподобността на връзката се предопределя от нивото на достигнатото познанието за явленията 2;
- Когато тя се потвърждава и в други сродни проучвания, тоест има устойчив характер.
- Когато времевата последователност на причината и следствието съответства на специфичния механизъм на взаимодействията между явленията 3.
Основни понятия
В настоящия курс са разгледани най-улеснените видове статистически връзки - тази между две променливи. Връзката между два количествени признака (нп. тегло, ръст, кръвно налягане) се означава като корелация и се изследва с помощта на корелационен анализ. Връзката между два качествени признака (нп. пол, заболеваемост, тютюнопушене, диагноза) се изследва с помощта на теста за асоциация.
Статистическата връзка се изследва в обема на наличните данни от извадката. Предположението и в по-широк мащаб и при стойности извън наличните в извадката е пример за екстраполация 4.
Екстраполацията е математически метод за намиране на нови стойности на конкретна променлива, следствие на установена статистическа връзка, които са извън интервала при нейното построяване.
Асоциация
Тестът за оценка на връзка между две качествени променливи се нарича \({\chi^2}\) тест за асоциация. Той е един от най-често използваните в медицинската статистика. Тестът протича в следната последователност от стъпки:
- Дефиниране на нулева и алтернативна хипотеза;
- Определяне на ниво на грешка;
- Изчисляване на теоретични честоти;
- Изчисляване на стойността на \({\chi^2}\);
- Определяне на p-стойност;
- Заключение.
За прилагането му е представен следния пример:
Да приемем, че в проучване се тестват три вида лекарства за лечение на КОВИД-19. Медикаментите са означени като “А”, “В” и “C”. В изследването са включени 500 пациенти, от които лекувани с “А” са 150, с “В” - 250, а с “С” - 100. След 1 месец са установени следните резултати от терапията - починали са 180, с частично подобрение - 220, а напълно оздравели са 100. Резултатите са представени в Таблица 1 и на Фигура 1.
| л-вство | починали | подобрение | оздравели | \(\sum_{rows}\) |
|---|---|---|---|---|
| А | \({f_o{a}}\) 65 | \({f_o{d}}\) 70 | \({f_o{g}}\) 15 | 150 |
| В | \({f_o{b}}\) 100 | \({f_o{e}}\) 110 | \({f_o{h}}\) 40 | 250 |
| С | \({f_o{c}}\) 15 | \({f_o{f}}\) 40 | \({f_o{i}}\) 45 | 100 |
| \(\sum_{columns}\) | 180 | 220 | 100 | 500 |
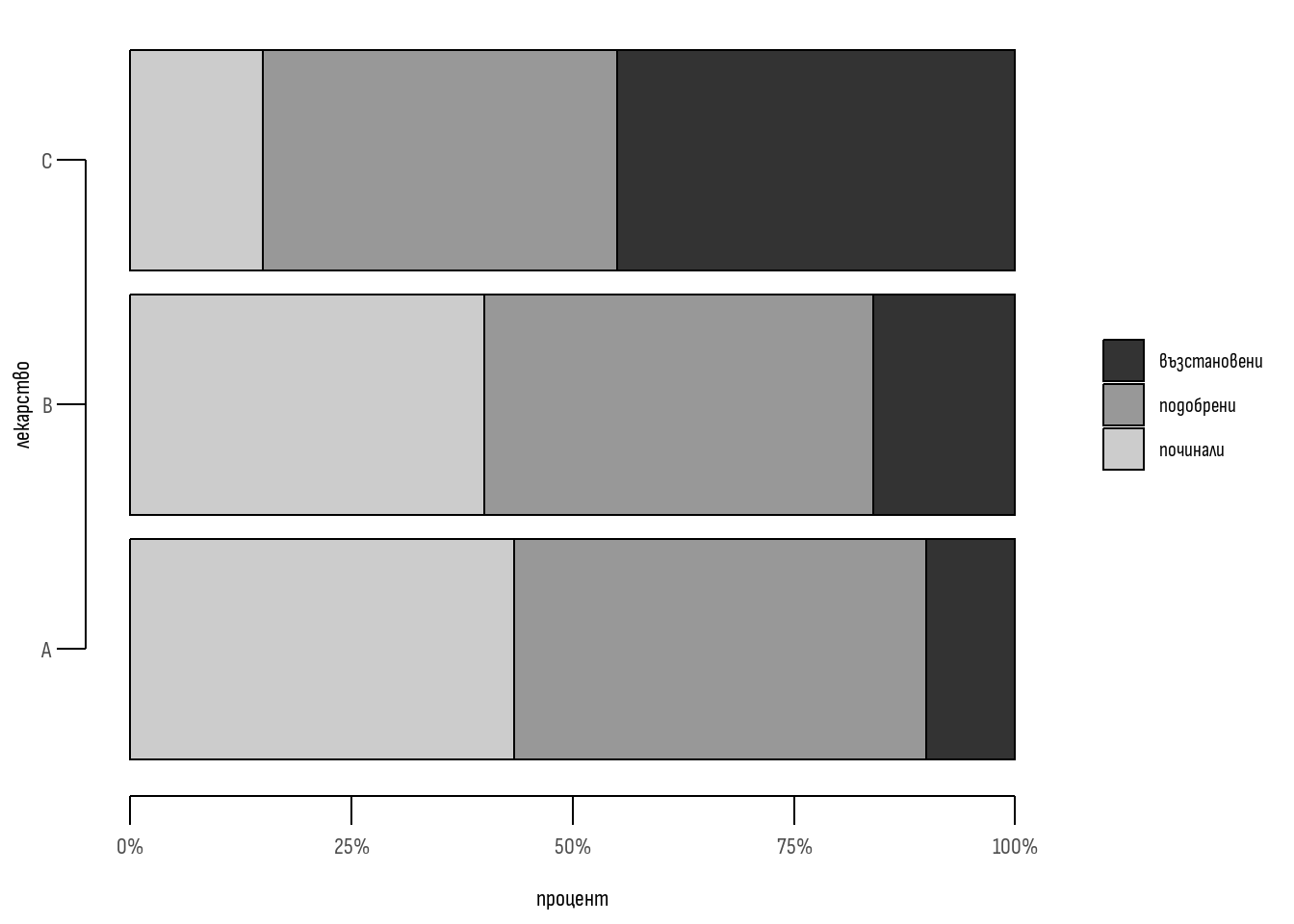
Числата, записани във всяка една от клетките на Таблица 1 (a, b, c и т.н) се наричат наблюдавани или обсервирани честоти. Те се бележат със символа \({f_o}\) и са в резултат от действително наблюдаваните резултати от клиничното проучване.
Дефиниране на хипотези
- Нулевата хипотеза
-
твърди, че не съществува асоциация (връзка) между вида на терапията и резултата от лечението 5.
- Алтернативната хипотеза
-
е противоположна на нулевата и твърди, че същества асоциация между лекарството и резултата от лечението.
Ниво на грешка
За ниво на грешка в повечето медицински проучвания се използва стойността 0,05. Това означава, че при бихме отхвърлили нулевата хипотеза, само ако вероятността тя да е вярна (да се наблюдавали връзката случайно) е по-малка от 0,05.
За всички останали клетки \[{f_t}b = \frac{180\cdot250}{500} = 90\]
\[{f_t}c = \frac{180\cdot100}{500} = 36\]
\[{f_t}d = \frac{220\cdot150}{500} = 66\]
\[{f_t}e = \frac{220\cdot250}{500} = 110\]
\[{f_t}f = \frac{220\cdot100}{500} = 44\]
\[{f_t}g = \frac{100\cdot150}{500} = 30\]
\[{f_t}h = \frac{100\cdot250}{500} = 50\]
\[{f_t}i = \frac{100\cdot100}{500} = 20\]
Изчисляване на теоретични честоти
Теоретичните честоти са числата (стойностите) на клетките (a, b, c и т.н), които бихме наблюдавали, ако нулевата хипотеза е вярна. Те се изчисляват по следната формула:
\[{f_t}cell = \frac{{\sum_{columns}}\cdot{\sum_{rows}}}{\sum_{total}}\]
Където:
- \({f_t}cell\) е теоретична честота за всяка една клетка;
- \(\sum_{columns}\) е сумата по колоните;
- \(\sum_{rows}\) е сумата по редовете;
- \(\sum_{total}\) е общата сума (всички участници);
Нека приложим формулата за първата клетка “а”:
\[{f_t}a = \frac{180\cdot150}{500} = 54\]
Теоретичната честота \({f_t{a}}\) означава, че ако липсва връзка между лечението и резултата, починалите пациентите лекувани с терапия “А” трябва да бъдат 54. Резултатите за всички клетки са представени в Таблица 2 и на Фигура 2.
| л-вство | починали | подобрение | оздравели | \(\sum_{rows}\) |
|---|---|---|---|---|
| А | \({f_t{a}}\) 54 | \({f_t{d}}\) 66 | \({f_t{g}}\) 30 | 150 |
| В | \({f_t{b}}\) 90 | \({f_t{e}}\) 110 | \({f_t{h}}\) 50 | 250 |
| С | \({f_t{c}}\) 36 | \({f_t{f}}\) 44 | \({f_t{i}}\) 20 | 100 |
| \(\sum_{columns}\) | 180 | 220 | 100 | 500 |
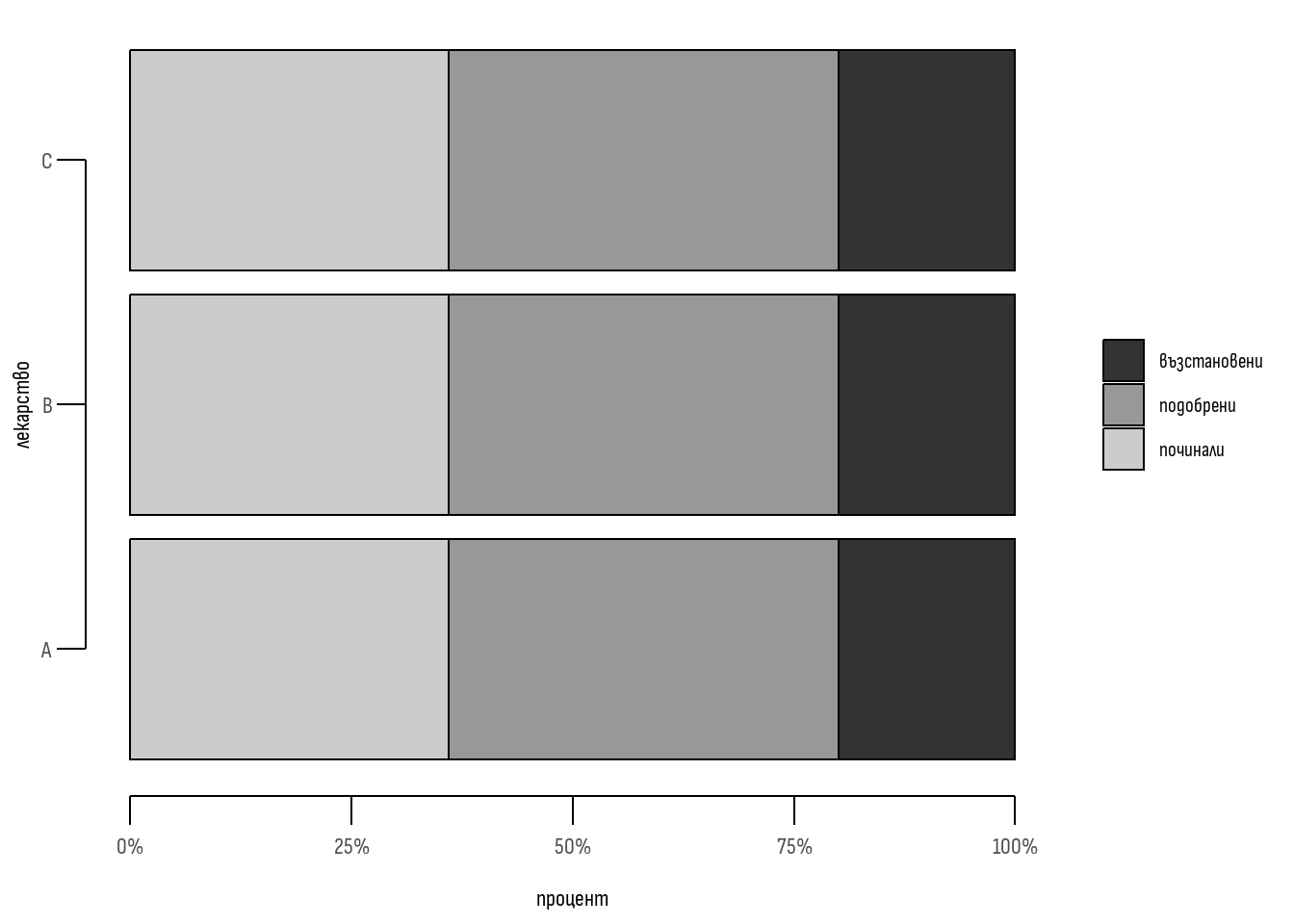
Изчисляване на стойността на \({\chi^2}\)
Във формулата:
- \({\chi^2}\) е стойността на хи-квадрат;
- \({f_0}\) е наблюдаваната честота за всяка една клетка (а, b, c и т.н);
- \({f_t}\) е теоретичната честота за всяка една клетка (а, b, c и т.н);
- \({f_0}-{f_t}\) е разликата между наблюдаваната и теоретичната честота за всяка една клетка (а, b, c и т.н);
- \(({f_0}-{f_t})^2\) е разликата повдигната на квадрат;
- \(\frac{({f_0}-{f_t})^2}{f_t}\) е делимото на повдигната на квадрат разлика спрямо теоретичната честота за всяка една клетка (а, b, c и т.н);
- \(\sum\) е сумата от всички разделяния.
Очевидно има разлика между очакванията на нулевата хипотеза (Таблица 2) и реалните данни (Таблица 1). За да се измери до каква степен наблюдаваните данни се различават от теоретичните честоти и да се оцени силата на връзка между изследваните променливи (вид лечение и клиничен резултат) се използва показателя \({\chi^2}\) (хи-квадрат).
Формулата е:
\[{\chi^2}=\sum\frac{({f_0}-{f_t})^2}{f_t}\]
В примера:
\[{\chi^2}=\frac{(65 – 54)^2}{54}+ \frac{(100 – 90)^2}{90}+\frac{(15 – 36)^2}{36}+\frac{(70 – 66)^2}{66}+\frac{(110 – 110)^2}{110}+\]
\[\frac{(40 – 44)^2}{44}+\frac{(15 – 30)^2}{30}+\frac{(40 – 50)^2}{50}+\frac{(45 – 20)^2}{20}\]
\[{\chi^2}=\frac{11^2}{54}+\frac{10^2}{90}+\frac{(-21)^2}{36}+\frac{4^2}{66}+\frac{0^2}{110}+\frac{(-4)^2}{44}+\frac{(-15)^2}{30}+\frac{(-10)^2}{50}+\frac{25^2}{20}\]
\[{\chi^2}=\frac{121}{54}+\frac{100}{90}+\frac{441}{36}+\frac{16}{66}+\frac{0}{110}+\frac{16}{44}+\frac{225}{30}+\frac{100}{50}+\frac{625}{20}\]
\[{\chi^2}=2.24+1.11+12.25+0.24+0+0.36+7.5+2+31.25 = 56.95\]
Стойността 54 е оценка на “несъответствието” между това, което нулевата хипотеза твърди и това, което ние действително сме наблюдавали.
Определяне на p-стойност
Следва да се определи, каква е вероятността това несъответствие да е чиста случайност \(p\). По подобие на t стойността в упражнение 3, отново се използва таблица, с известни стойности \({\chi^2}\) и съответните им вероятности \(p\). Преди тази стъпки трябва да определялият “степените на свобода” \({df}\). От тях зависи точния ред на статистическата таблица за \({\chi^2}\) разпределението, който трябва да се използва за всеки конкретен пример.
Във формулата:
- \({N_{columns}}\) е броят на колоните;
- \({N_{rows}}\) е броят на редовете;
\({df}\) е число, което зависи от размера на таблично представените данни - броя на колоните и редовете и се изчисляват по формулата:
\[{df}=({N_{columns}}-1)\cdot({N_{rows}}-1)\]
В посочения пример - таблицата е с 3 колони и 3 реда (таблица 3х3).
Степените на свобода са: \[{df}=(3-1)\cdot(3-1)=2\cdot2=4\]
| df | p = 0.1 | p = 0.05 | p = 0.01 |
|---|---|---|---|
| 4 | \({\chi^2}\) =7.779 | \({\chi^2}\) =9.488 | \({\chi^2}\) =13.27 |
В Таблица 3 са представени данните само за реда, съответстващ на \({df}=4\). За всяка стойност на \({\chi^2}\) е определена вероятността \(p\).
В тази стъпка сравняваме изчислената стойност на \({\chi^2}=56.95\) с наличните данни. Въпреки че точната стойност не е налична в Таблица 3, тя е по-голяма от най-дясно разположеното число - 13.27, което съответства на вероятност \(p\) 0.01.
С увеличаването на стойността на \({\chi^2}\), вероятността \(p\) намалява.
Заключение
\({\chi^2}=57\) е по-голямо от 13.27, което означава, че вероятността \(p\) е по-малка от нивото на грешка 0.05. Следователно - отхвърляме нулевата хипотеза и приемаме алтернативната. Има статистически значима връзка (зависимост) между избраното лечение и клиничния резултат.
Малко повече за асоциацията
- За да прилагаме този тест е необходимо да имаме поне 5 наблюдения във всяка една клетка. При по-малки стойности не можем да се доверим на получената стойност за \(p\).
- Когато работим с качествени (алтернативни) признаци с две възможни стойности (таблици 2х2) може да се използва разновидност на корелационния анализ. Коефициентът в случая се означава с символът \({\phi}\) 6, а пример за неговото приложение е представен в Таблица 4.
| Ваксина | Имунен отговор | Без имунен отговор |
|---|---|---|
| Нова | “а” 90 | “c” 10 |
| Стара | “b” 160 | “d” 90 |
Където:
- \({\phi}\) е коефициентът на корелация;
- “а” е броят на ваксинираните с новата ваксина и придобили имунитет;
- “b” е броят на ваксинираните с старата ваксина и и придобили имунитет;
- “c” е броят на ваксинираните с новата ваксина и не придобили имунитет;
- “d” е броят на ваксинираните със старата ваксина и не придобили имунитет;
\[{\phi}=\frac{(a\cdot{d})-(b\cdot{c})}{\sqrt{(a+b)\cdot(c+d)\cdot(a+c)\cdot(b+d)}}\] В примера:
\[{\phi}=\frac{(90\cdot90)-(160\cdot10)}{\sqrt{(90+160)\cdot(10+90)\cdot(90+10)\cdot(160+90)}}\]
\[{\phi}=\frac{(8100)-(1600)}{\sqrt{(250)\cdot(100)\cdot(100)\cdot(250)}}\]
\[{\phi}=\frac{6500}{\sqrt{62500000}} =\frac{6500}{7906.25}=0.82\]
Корелация
Статистически метод, използван за изследване на взаимовръзка между две количествени променливи
Корелационен коефициент
Корелационният коефициент е число в диапазона от -1 до +1. Колкото по отдалечена е стойността му от 0 -лата, толкова по-силна е наблюдаваната статистическа връзка. Съществуват множество методики и видове корелационнни коефициенти, въпреки това целта на всички тях е:
- Да оцени силата на статистическата връзка
- Да се оцени посоката на връзката 7;
- Да се определи формата на връзката 8;
Коефициент на Пирсън
В настоящият курс е представен само един от множеството коефициенти за корелация - този на Пирсън, който се означава с гръцката буква \({\rho}\) или с латинската \({r}\). Коефициентът е подходящ, когато изследваните променливи са нормално разпределени, а предполагаемата връзката между тях е линейна. Интерпретацията на коефициента на Пирсън е представена в Таблица 5.
| \({\rho}\) | сила и посока на връзката |
|---|---|
| 1 | “перфектна” права |
| 0.67 до 1 | силна права |
| 0.34 до 0.66 | умерена права |
| 0 до 0.33 | слаба права |
| 0 | липсва връзка |
| 0 до - 0.33 | слаба обратна |
| - 0.34 до -0.66 | умерена обратна |
| - 0.67 до - 1 | силна обратна |
| -1 | “перфектна” обратна |
Изчисление на коефициента на Пирсън
\({\rho}\) се изчислява с помощта на следната формула:
\[{\rho}=\frac{ \sum_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y}) }{\sqrt{\sum_{i=1}^{n}(x_i-\bar{x})^2}\sqrt{\sum_{i=1}^{n}(y_i-\bar{y})^2}}\]
Където:
- \(x_i\) и \(y_i\) са стойностите на променливите x и y за всеки един от участниците в изследването;
- \(\bar{x}\) и \(\bar{y}\) са средните аритметични за променливите x и y;
- \(x_i-\bar{x}\) е отклонението на всяка една точка от средната аритметична за променливата x;
- \(y_i-\bar{y}\) е отклонението на всяка една точка от средната аритметична за променливата y;
- \(\sum_{i=1}^{n}(x_i-\bar{x})^2\) е сумата на квадратите на отклоненията за променливата x;
- \(\sum_{i=1}^{n}(y_i-\bar{y})^2\) е сумата на квадратите на отклоненията за променливата y;
| име | Ръст (x) | Тегло (y) |
|---|---|---|
| Мария | 160 | 50 |
| Иван | 170 | 90 |
| Чавдар | 180 | 100 |
Пример за изчисление на коефициента на Пирсън
Формулата може да се представи като последователност от стъпки. Нека приемем, че разполагаме с данните за ръста и теглото на 3 студенти и следва да определим корелацията между тези две количествени променливи. Данните са представени в Таблица 6 и на Фигура 3.
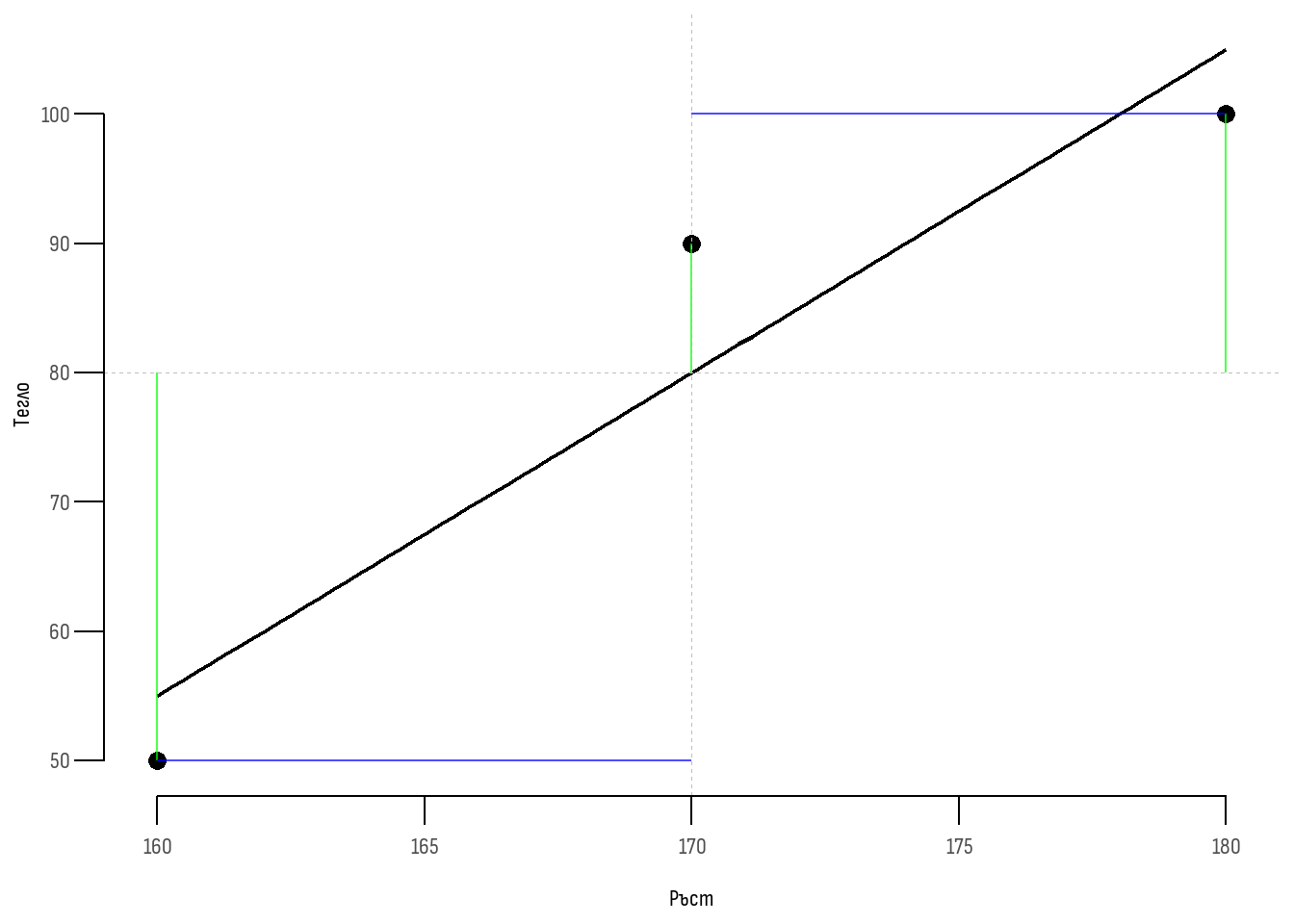
Стъпка 1 - изчисляване на средната аритметична
Изчисляваме средната аритметична, както за променливата х (ръста), така и за променливата у (теглото).
за ръста \[\bar{x}=\frac{160+170+180}{3}=170\]
за теглото \[\bar{y}=\frac{50+90+100}{3}=80\]
Стъпка 2 - Изчисляване на отклоненията
Отклоненията представляват разликата между стойността на наблюденията и средната аритметична за групата.
За втория студент (Иван) тези отклонения са:
\[x_{i=2}-\bar{x}=170-170=0\] \[y_{i=2}-\bar{y}=90-80=10\]
За третия студент (Чавдар) тези отклонения са:
\[x_{i=3}-\bar{x}=180-170=10\] \[y_{i=3}-\bar{y}=100-80=20\]
За първия студент (Мария) тези отклонения са:
за ръста \[x_{i_1}-\bar{x}=160-170=-10\]
за теглото \[y_{i=1}-\bar{y}=50-80=-30\]
В Таблица 7 са представени резултатите от тази стъпка за всички наблюдавани студенти.
| име | Ръст | Тегло | \((x-\bar{x})\) | \((y-\bar{y})\) |
|---|---|---|---|---|
| Мария | 160 | 50 | -10 | -30 |
| Иван | 170 | 90 | 0 | 10 |
| Чавдар | 180 | 100 | 10 | 20 |
| \(\bar{x}\) = 170 | \(\bar{y}\) = 80 |
Стъпка 3 - Изчисляване на кръстосания продукт
В трета стъпка се определя “сумата на кръстосания продукт.” Под “кръстосан продукт” се разбира умножението на отклоненията за всяка една от променливите.
\[\sum_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y})\].
За втория студент (Иван):
\[(x-\bar{x})\cdot(y-\bar{y})=(0)\cdot(10)=0\]
За третия студент (Чавдар):
\[(x-\bar{x})\cdot(y-\bar{y})=(10)\cdot(20)=200\]
За първия студент (Мария) кръстосаният продукт е:
\[(x-\bar{x})\cdot(y-\bar{y})=(-10)\cdot(-30)=300\]
Таблица 8 представя таблично резултатите от тази стъпка и сумата на кръстосаните произведения за всички наблюдавани студенти.
| име | Ръст | Тегло | \((x-\bar{x})\) | \((y-\bar{y})\) | \((x-\bar{x})\cdot(y-\bar{y})\) |
|---|---|---|---|---|---|
| Мария | 160 | 50 | -10 | -30 | 300 |
| Иван | 170 | 90 | 0 | 10 | 0 |
| Чавдар | 180 | 100 | 10 | 20 | 200 |
| \(\bar{x}\) = 170 | \(\bar{y}\) = 80 | \(\sum\) = 500 |
Стъпка 3 предоставя числителя на посочената по-горе формула. В използвания пример той е равен на 500.
Стъпка 4 - Изчисляване на сумата на квадратите на отклоненията
Стъпка 4 се използва за определяне на знаменателя на посочената формула. В нея, изчисляваме сумата на квадратите на отклоненията за всяка една променлива - \({(x-\bar{x})^2}\) и \({(y-\bar{y})^2}\).
Самите отклонения са изчислени в стъпка 2 и представени в Таблица 7. В този етап, те се повдигат на квадрат и сумират, както е представено в Таблица 9.
| име | Ръст | Тегло | \((x-\bar{x})\) | \((x-\bar{x})^2\) | \((y-\bar{y})\) | \((y-\bar{y})^2\) |
|---|---|---|---|---|---|---|
| Мария | 160 | 50 | -10 | 100 | -30 | 900 |
| Иван | 170 | 90 | 0 | 0 | 10 | 100 |
| Чавдар | 180 | 100 | 10 | 100 | 20 | 400 |
| \(\bar{x}\) = 170 | \(\bar{y}\) = 80 | \(\sum\) = 200 | \(\sum\)=1400 |
Стъпка 5 - Изчисляване на корелационния коефициент
Вече сме готови за заместим във формулата:
\[{\rho}=\frac{\sum_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y}) }{\sqrt{\sum_{i=1}^{n}(x_i-\bar{x})^2}\sqrt{\sum_{i=1}^{n}(y_i-\bar{y})^2}}\]
\[{\rho}=\frac{500}{\sqrt{200}\cdot{\sqrt{1400}}}\]
\[{\rho}=\frac{500}{{14.1}\cdot{37.42}}=\frac{500}{529}=0.94\]
Стъпка 6 Заключение
При тези трима студенти се наблюдава силна позитивна корелация между ръста и теглото - увеличението на теглото се свързва с увеличение на ръста. Връзката е валидна само за тези трима студенти. За да установим дали има такава в генералната съвкупност, провеждаме тест на хипотеза 9
В случая:
- Нулевата хипотеза
-
твърди, че популационният корелационен коефициент е нула. С други думи не същества корелация между теглото и ръста.
- Алтернативната хипотеза
-
твърди, че че в действителност има корелация и тя не е равна на 0-ла.
За да тестваме нулевата хипотеза, използваме тест подобен на вече известния Т теста.
Тестове и задачи за самоподготовка
Задачи
Задача 1
Като използвате непараметричен тест хи квадрат проверете съществува ли асоциация между продължителността трудовия стаж при миньорите и заболеваемостта от вибрационна болест?
| трудов стаж | с вибрационна болест | здрави | Общо |
|---|---|---|---|
| до 5г. | 32 | 127 | 159 |
| 6-15г. | 56 | 268 | 324 |
| 16-25г. | 23 | 48 | 71 |
| над 25г. | 41 | 34 | 75 |
| Общо | 152 | 477 | 629 |
Задача 2
При проучване на влиянието на вида използван дюшек при получаване на декубитусни рани, са получени следните резултати:
- При low air-loss дюшек при 7 от 56 изследвани случаи имат декубитусни рани
- При воден дюшек при 13 от 71 изследвани лица
- При дюшек на вълни с декубитусни рани са 25 от 72 пациенти
Определете дали видът на използвания дюшек е фактор за появата на декубитосни рани?
Задача 3
При проучване на нов анестетик е отчетено времето от подаването му във венозната система до реакцията на пациента и съответната ефективна доза, определена в ug/kg.
| доза | време за въздействие |
|---|---|
| 1,3 | 25 |
| 1,9 | 13 |
| 1,5 | 19 |
| 1,1 | 23 |
| 1 | 26 |
| 1,3 | 21 |
| 2,1 | 11 |
| 1,7 | 30 |
| 1,6 | 14 |
| 0,9 | 24 |
| общо: 14,4 | общо: 206 |
Първо:
Изчислете 95% -вия интервал на доверителност на ефективна доза в генералната съвкупност.
Второ:
Изчислете 95% -вия интервал на доверителност за времето до ефект в генералната съвкупност.
Трето:
Докажете дали съществува връзка между явленията доза и време за реакция.
Тестове
- Кой вид диаграма е най-подходящ за представяне на връзката между 2 количествени променливи?
- Комбинирана диаграма на разсейването (scatterplot)
- Стълбовидна диаграма (bar chart)
- Хистограма
- Кръгова диаграма (pie chart)
- Корелационен коефициент r = -0.10 означава:
- Силна обратна причинно-следствена връзка.
- Умерена обратна причинно-следствена връзка.
- Слаба обратна причинно-следствена връзка.
- Всички отговори са грешни.
- Кое от следните твърдения е вярно?
- Интерполацията прогнозира извън област от вече известни стойности, които са послужили за конструиране на регресионен модел.
- При равни други условия, екстраполацията постига по-голяма валидност на получената оценка в сравнение с интерполацията.
- Екстраполацията поставя условие наблюдаваната зависимост да се запази извън областта от вече известните стойности.
- Графичният образ на еднофакторните нелинейни модели са различни прави в равнината.
- Фи коефициентът за корелация на Пирсън се използва при анализ на връзката между:
- 2 количествени променливи.
- 2 дихотомни променливи.
- 1 количествена и 1 качествена променливи.
- 1 количествена и 1 дихотомна променливи.
- Корелационен коефициент r = -1.2 означава:
- Силна обратна зависимост.
- Умерена обратна зависимост.
- Слаба обратна зависимост.
- Всички отговори са грешни.
Отворени въпроси
Проучване на нивото на затлъстяване (дефинирано като „предзатлъстяване” „затлъстяване I степен” „затлъстяване II степен” и „затлъстяване III степен”) при пушачи и непушачи достига до резултат χ2 = 9.488 / df = 4. На колко е равна р-стойността в този случай и какво означава това? Какъв извод може да се направи въз основа на този резултат?
Проучване на нивото на затлъстяване при пушачи и непушачи достига до резултат χ2 = 15.507 / df = 8. На колко е равна р-стойността в този случай и какво означава това? Какъв извод може да се направи въз основа на този резултат?
Бележки
В повечето случаи, взаимоотношенията в областта на биологията, медицината и здравеопазването са твърде сложни, за да се обяснят единствено със статистическите коефициенти.↩︎
Липсата на научни знания за механизма на взаимоотношенията обаче не означава, че причинно-следственият характер на връзката трябва да бъде отхвърлен.↩︎
Проверката по този критерий може да не бъде толкова лесна и проста задача, колкото изглежда на пръв поглед. Понякога трябва да се преодолеят редица трудности, за да се маркират времевите моменти на причинно-следствените промени↩︎
Да приемем, че в една извадка (предимно с деца) сме наблюдавали връзка между увеличаването на теглото и увеличаването на ръста. Същата връзка обаче не бива да се екстраполира при възрастните - при тях растежът на височина е завършил, а теглото може да се увеличава (понякога и безконтролно).↩︎
С други думи, каквото и хапче да даваме на тези пациенти, резултатът е един и същ, а ако наблюдаваме някаква разлика, тя е следствие на случайност.↩︎
\({\phi}\) се интерпретира, както коефициентът на Пирсън - обяснен по-надолу.↩︎
Права връзка (позитивна корелация) се наблюдава, когато двете променливи се увеличават или намалят синхронно. Негативна корелация (обратна връзка) се наблюдава, когато увеличението в една променлива е свързано с намаление в другата.↩︎
Връзката може да е “линейна” още пропорционална или “нелинейна” - експоненциална, логаритмична и т.н. В този курс ще се спрем единствено на линейната връзка.↩︎
Тестът на хипотеза за корелационния коефициент не е обект на настоящия курс.↩︎